Satz von Stiller: Unterschied zwischen den Versionen

Aus MünsterWiki
 
(4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
−
[[Datei:Pascal-6points-s.svg|300px|mini|Der [[Satz von Pascal]] ist nachweislich falsch]]
+
Der '''Satz von Stiller''' (nach [[Joachim Stiller]]) ist eine Aussage über ein 6-Eck auf einem regelmäßigen Viereck (Parallelogramm) in einer projektiven Ebene. Er lässt sich auch in der reellen affinen Ebene formulieren. Dmit ist der Satz von Pascal eindeutig wiedelegt, und zwar durch rein geoemtrishen Beweis. q.e.d.
 +
 
 
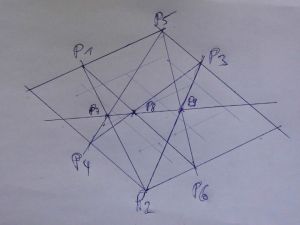
[[Datei:Bild z 41.jpg|thumb|300px|Der Satz von Stiller am regelmäßigen Viereck (Parallelogramm)]]
 
[[Datei:Bild z 41.jpg|thumb|300px|Der Satz von Stiller am regelmäßigen Viereck (Parallelogramm)]]
 
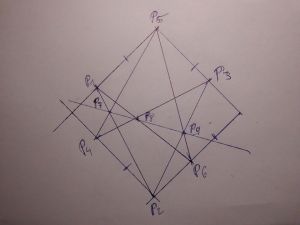
[[Datei:Bild z 43.jpg|thumb|300px|left|Der Satz vin Stiller am Quadrat - alle drei Schnittpunkte liegen auf einer Geraden.]]
 
[[Datei:Bild z 43.jpg|thumb|300px|left|Der Satz vin Stiller am Quadrat - alle drei Schnittpunkte liegen auf einer Geraden.]]
Zeile 5: Zeile 6:
 
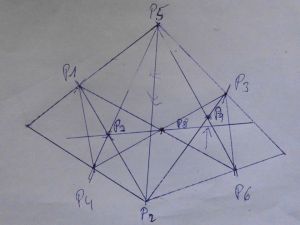
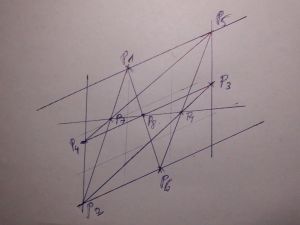
[[Datei:Bild z 44.jpg|thumb|300px|left|Der Satz von Stiller noch einmal am Parallelo- gramm. Es geht "immer".]]
 
[[Datei:Bild z 44.jpg|thumb|300px|left|Der Satz von Stiller noch einmal am Parallelo- gramm. Es geht "immer".]]
  
−
Der '''Satz von Stiller''' (nach [[Joachim Stiller]]) ist eine Aussage über ein 6-Eck auf einem regelmäßigen Viereck (Parallelogramm) in einer [[Projektive Ebene|projektiven Ebene]]. Er lässt sich in der reellen affinen Ebene wie folgt formulieren:
+
[[Kategorie:Geometrie]]
−
 
+
[[Kategorie:Joachim Stiller]]
−
Für paarweise gegenüberliegende 6 Punkte <math>P_1,P_2,P_3,P_4,P_5,P_6 </math> eines regelmäßigen Vierecks (Parallelogramm) in einer projektiven Ebene liegen die Punkte
 
−
: <math> P_7:= \overline{P_1P_2}\cap \overline{P_4P_5},</math>
 
−
: <math> P_8:= \overline{P_6P_1}\cap \overline{P_3P_4},</math>
 
−
: <math> P_9:= \overline{P_2P_3}\cap \overline{P_5P_6}</math>
 
−
auf einer Geraden, der '''Stiller-Geraden''' (s. Bild unten).
 
−
 
 
−
[[Kategorie:Synthetische Geometrie]]
 
−
[[Kategorie:Projektive Geometrie]]
 
−
[[Kategorie:Satz (Mathematik)]]
 
−
[[Kategorie:Affine Geometrie]]
 
−
[[Kategorie:Ebene Geometrie]]
 

Aktuelle Version vom 21. September 2025, 16:26 Uhr

Der Satz von Stiller (nach Joachim Stiller) ist eine Aussage über ein 6-Eck auf einem regelmäßigen Viereck (Parallelogramm) in einer projektiven Ebene. Er lässt sich auch in der reellen affinen Ebene formulieren. Dmit ist der Satz von Pascal eindeutig wiedelegt, und zwar durch rein geoemtrishen Beweis. q.e.d.

Der Satz von Stiller am regelmäßigen Viereck (Parallelogramm)
Der Satz vin Stiller am Quadrat - alle drei Schnittpunkte liegen auf einer Geraden.
Am unregelmäßigen Viereck geht es leider "nicht". P9 fällt aud der Geraden heraus.
Der Satz von Stiller noch einmal am Parallelo- gramm. Es geht "immer".
Abgerufen von „http://muensterwiki.de/index.php?title=Satz_von_Stiller&oldid=70477“